前言

Geogebra是一款非常强大的理科演示工具，可以广泛地用于数学或物理教学或仿真，相信肯定有很多朋友想要学习但不知如何下手。这里就分享一下我认为比较好的Geogebra的学习路线，相信可以帮助你少走弯路。首先说一下Geogebra真的非常简单好上手，它比任何一种编程语言都简单，相信你在半天时间就可以掌握它的基础操作，并能够顺利制作你所需要的课件。

软件下载

Geogebra主要有两个版本，GGB5和GGB6。

GGB5基于Java开发制作，性能更好且高效，界面简洁，适合老手和喜欢用代码写程序的老师。

GGB6是Java打包的javascript版本，界面更加美观，且有比较好的代码提示功能，适合新手入门。缺点就是性能没有GGB5好。

软件都可以访问https://ggb123.cn/download进行下载。

学习方法

1. GGB学习的最好方法就是多思多做。
2. GGBTool提供了很多学习过程中的实用工具，比如指令查询、GGB程序搜索，可以提高你的学习效率。
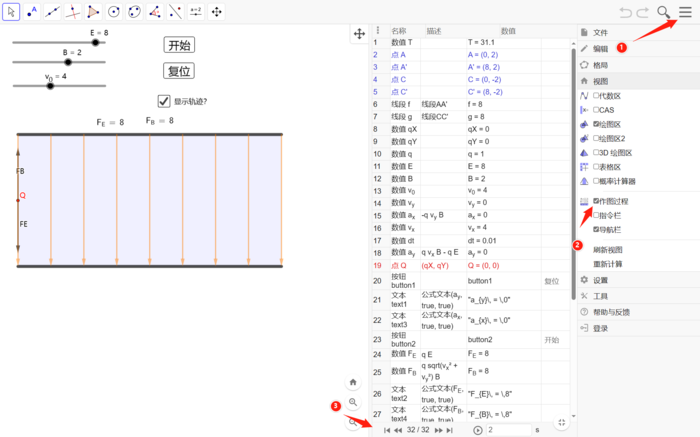
3. 你可以利用GGB自带的作图过程功能，重现小程序一步步制作出来的过程，进行理解学习。方法如下：
   
4. 可以加一些GGB学习群，自己实在解决不了的问题可以尝试在群中礼貌询问求解。

学习路线

学习路线概括如下：

1. 熟悉软件和基本操作

强烈推荐 唐大仕老师在慕课网推出的免费教程 ，质量很高且免费。
点击第几次开课可以看到历史开课记录，比较靠后的可能看不了，你可以查看前几次比如第5次开课，就可以看到完整内容了，内容都差不多。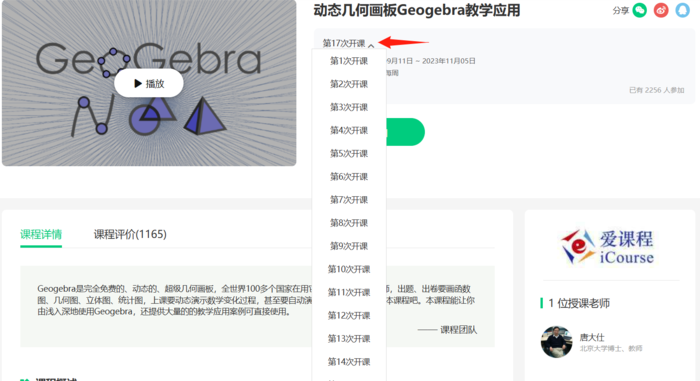

可以开二倍速看。

2. 在跟做中学习了解常见指令

第1步完成以后相信你可以做出一个比较不错的GGB课件了，但是你还需要掌握更多的指令，你所掌握的指令越多，GGB用的就会越熟练。擅用GGBTool中的GGB指令查询功能（唐大仕老师开发），可以大大提高指令学习效率。

张成进老师制作了一个GGB-高中物理入门教程，里面举例说明了常用指令和新手常见问题，非常值得一看：

你可以在Geogebra官网搜索你需要的GGB小程序，然后利用GGB的作图过程功能跟着实现重做。

除此之外还推荐一些教程：

1. B站物理罗老师的视频教程（免费）
   https://space.bilibili.com/562460538
2. 张成进老师的GGB教程
   张老师制作了各个板块的高中物理的GGB模型，并且给出了制作步骤，非常适合新手跟做。
   购买可咨询QQ82899594

学习资源

1.唐家军老师编著的《GeoGebra5使用手册》
该书详细介绍了GGB5的使用，是一本非常详细的GGB5使用说明书

2.唐家军老师编著的《GeoGebra指令汇编》
该书详细介绍了GGB的几乎全部指令，可以作为手册翻查